[ つぎ | うえ | まえ ]
つぎに 3 次元の座標で考えよう。3 次元の回転は,2 次元の座標平面を 単に,x 軸に対して(y-z 平面)、 y 軸に対して(z-x 平面),z 軸に対して(x-y 平面) に分けて考えればよい。 x 軸回りの回転は,y-z 平面に 対して,x を原点をみれば,2 次元の回転に帰着することができる.

ここで,3 次元座標平面上の点 (x1,y1,z1) を αラジアン回転した座標を (x2,y2,z2) とすると,以下のようになる.
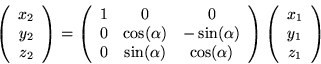
同様に,y 軸に対して βラジアン回転した場合を考えることができる.

3 次元座標平面上の点 (x2,y2,z2) を y 軸に対して,βラジアン回転した座標を (x3,y3,z3)とすると,以下のようになる.

さらに,z 軸に対して同様の議論ができる.

3 次元座標平面上の点 (x3,y3,z3) を z 軸に対して,γラジアン回転した座標を (x4,y4,z4)とすると,以下のようになる.
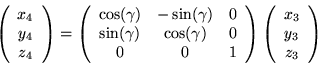
このように回転した点を,例えば,平面 z = 0 に平行投影した図形を 画面に表示させればよい(画面は,2 次元である). 平行投影では,無限遠のかなたから,人間がみていると考えれば, その図形に歪みはなく簡単に考えることができる. つまり,単に,z 座標を忘れて,x,y 座標だけを使って画面に描けばよい.
これで,準備がととのった!
そして,表示するものを「回転体」としよう.回転体も同じように,これらの 概念を使ってデータを計算することができる.
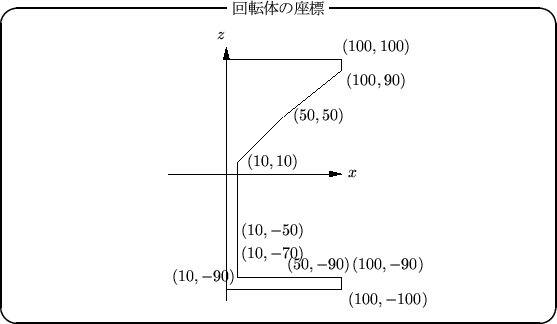
例えば,上の z-x 平面に書かれた点の座標を使って,z 軸に回転した回転 体を考える.これを x-y 平面に平行投影して表示してみると,以下のようになる.
さらに,x-z 平面に平行投影して表示してみると,以下のようになる.
この回転体が,ひっくりかえってみえるのは,数学で示す座標が,下から上に 向かって,増加するのに対して,プログラムで表す座標が, 上から下に向かって増加するためである. もちろん,プログラムを修正することにより, それらを同じにすることができるが,ここでは,あえて素直にプログラミング してみた.
ソースコードは,以下の通りである.
Last update: Thu Aug 15 16:27:08 PDT 2013 by