その3
[ つぎ | まえ | うえ ]
次に,無理数の値を求めてみよう.例えば 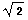 を求めてみよう.
無理数は有理数と違い,規則性のない無限小数として表現されるので何らかの工夫が必要である.
を求めてみよう.
無理数は有理数と違い,規則性のない無限小数として表現されるので何らかの工夫が必要である.
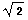 は, 方程式
は, 方程式 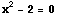 の解として与えられる。
の解として与えられる。 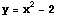 をグラフに表現すると以下のようになる。
をグラフに表現すると以下のようになる。
![]()
![[Graphics:Images1/index_gr_66.gif]](Images1/index_gr_66.gif)
![]()
点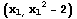 における接線の方程式は,
における接線の方程式は,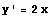 より
より 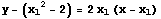 つまり,
つまり,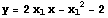 となる.
となる.
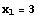 のときは
のときは 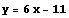 となる.
早速プロットしよう.
となる.
早速プロットしよう.
![]()
![[Graphics:Images1/index_gr_84.gif]](Images1/index_gr_84.gif)
![]()
この接線 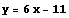 が,x 軸と交わる点は
が,x 軸と交わる点は 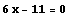 ,
, 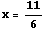 となる.
となる.
この x 座標 について接線を求めて,新たな x 軸との交点を求める。以下この繰り返しを行う。つまり
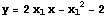 の
の 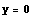 のとき,
つまり
のとき,
つまり 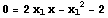 より,
より, 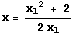 ,
, 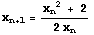 の繰り返しを行えばよい。
の繰り返しを行えばよい。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
このように,5 回の繰り返しにより,1.41421 になったことがわかる。
一般に,方程式 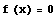 の解を求めるには,
の解を求めるには, 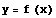 の
の 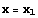 (初期値)における接線が
(初期値)における接線が
 軸と交わる点の
軸と交わる点の  座標を求め,
さらに,その x座標を元に, 次の x 座標を求め,というように
座標を求め,
さらに,その x座標を元に, 次の x 座標を求め,というように
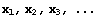 と点列を求めればよい。
このように
と点列を求めればよい。
このように 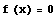 の解(近似値)を求める方法を,ニュートン法という。
の解(近似値)を求める方法を,ニュートン法という。
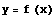 の
の 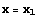 における接線の方程式は,
における接線の方程式は, 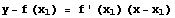 となり,
となり,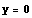 のとき,
のとき,
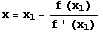 ,つまり
,つまり 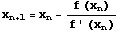 で求めることができる。この繰り返しを処理すればよい。微分は,Mathematica では簡単に求めることができる。
例えば,以下のように求めることができる.
で求めることができる。この繰り返しを処理すればよい。微分は,Mathematica では簡単に求めることができる。
例えば,以下のように求めることができる.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
これを使って上の漸化式を定義することができる.
![]()
![]()
![[Graphics:Images/index_gr_36.gif]](Images/index_gr_999.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Mathematica では,「ファイル」-> 「パレット」-> 「基礎的な入力」で微分の記号を入力することができる。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
この入力関数は自由に変更することができる.たとえば,√5を求めるには,以下のように入力すればよい。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
実はこのニュートン法の計算は,Mathematica の FindRoot 関数を使えば,簡単に求めることができる.
![]()
![]()
![]()
![]()
![]()
![]()
Last update: Thu Aug 15 16:27:08 PDT 2013 by