[ つぎ | うえ | まえ ]

---

はなしをまとめよう。今まで出てきた数式を以下のようにまとめてみる。

• 9x+5y ≦ 50
• x+5y ≦ 10
• x ≧ 0, y ≧ 0
• 5x+10y → max

結果、最大値 35

• 9x+5y ≦ 50
• x+5y ≦ 10
• 7x+20y ≦ 50
• x ≧ 0, y ≧ 0
• 5x+10y → max

結果、最大値 950/29

• 9x+5y ≦ 50
• x+5y ≦ 10
• 7x+20y ≦ 50
• x ≧ 0, y ≧ 0
• 3x+10y → max

結果、最大値 70/3

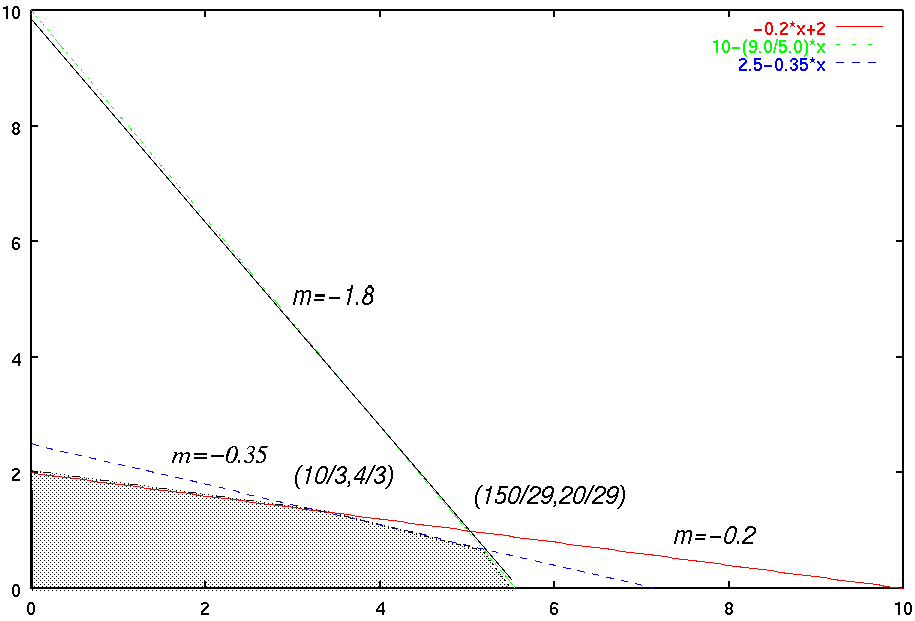
最後の2つの数式は、同じグラフに対して計算されるので目的関数の傾きにより最大値が異なる。

傾き	m < -1.8	m = -1.8	-1.8 < m < -0.35	m = -0.35	-0.35 < m < -0.2	m = -0.2	-0.2 < m ≦ 0
最大点	(50/9,0)	線分	(150/29,20/29)	線分	(10/3,4/3)	線分	(0,2)
最大値	1000/9		950/29		70/3		20

解説

などは、以下のように一般的に書くことができる。

• a₁₁x₁+a₁₂x₂+. . .+a_1nx_n≦ C₁
• a₂₁x₁+a₂₂x₂+. . .+a_2nx_n≦ C₂
• . . . . . .
• a_m1x₁+a_m2x₂+. . .+a_mnx_n≦ C_m
• b₁x₁+b₂x₂+. . . +b_nx_n→ max

ここで前半の m 個の式を制約条件，最後の 1 式を目的関数という。制約条件を満たす領域を許容領域という。 実は最小の場合も考えられるので、

• a₁₁x₁+a₁₂x₂+. . .+a_1nx_n≦ C₁
• a₂₁x₁+a₂₂x₂+. . .+a_2nx_n≦ C₂
• . . . . . .
• a_m1x₁+a_m2x₂+. . .+a_mnx_n≦ C_m
• b₁x₁+b₂x₂+. . . +b_nx_n → min

そこで，我々は m 個の制約条件で示される領域の範囲内で、 目的関数を満たす(実は，最小の場合もある)場合を求めることがここの目的であった。

ここで，ちょっと?

疑問が生じるかもしれない。今までの数式であつかった変数は x， y などの 2 変数であったが，3 変数以上の場合はどのように解くだろう?と．．．．．．

3 変数の場合は 3 次元の図を書けば求まることは求まるのであるが、手計算ではまず無理であろう。

実は，この問題は線形計画法とよばれ，最近ではコンピュータで簡単に解くことができる。Mathematica を使おう．

Copyright © 2000-2013 Hosei University.
Last update: Thu Aug 15 16:27:08 PDT 2013 by